Shapes play a crucial role in the field of geometry, where they are not only fundamental to mathematical principles but also essential to multiple disciplines such as art, architecture, and engineering. Among these shapes, the triangle and circle stand out due to their unique properties and interrelations. Triangles, with their structural efficiency, and circles, with their symmetry and elegance, offer rich avenues for exploration and practical application.
This article delves into the significance of triangles and circles, examining their definitions, mathematical relationships, geometric constructions, applications in real life, and theoretical concepts. Additionally, it will reveal fun facts about these shapes and their impact on various cultures throughout history.
Basic Definitions
Triangle
A triangle is a polygon with three edges and three vertices. It is one of the simplest forms of geometry but holds a complex hierarchical structure through its numerous types and properties.
– **Types of Triangles**:
– Equilateral Triangle: All three sides are equal, and all angles are equal (60 degrees).
– Isosceles Triangle: Two sides are equal, and the angles opposite to those sides are also equal.
– Scalene Triangle: All sides and angles are different.
– **Angles in a Triangle**:
– Acute Triangle: All angles are less than 90 degrees.
– Obtuse Triangle: One angle is greater than 90 degrees.
– Right Triangle: One angle is exactly 90 degrees.
Circle
A circle can be defined as the set of all points in a plane that are equidistant from a given point called the center.
– **Key Terms**:
– Radius: The distance from the center to any point on the circle.
– Diameter: Twice the radius; it is the longest chord of the circle.
– Circumference: The total distance around the circle, calculated as C = πD or C = 2πr.
– Area: The space enclosed within the circle, given by the formula A = πr².
– **Types of Circles**:
– Concentric Circles: Circles that share the same center but have different radii.
– Tangent Circles: Circles that touch at exactly one point.
Mathematical Relationships
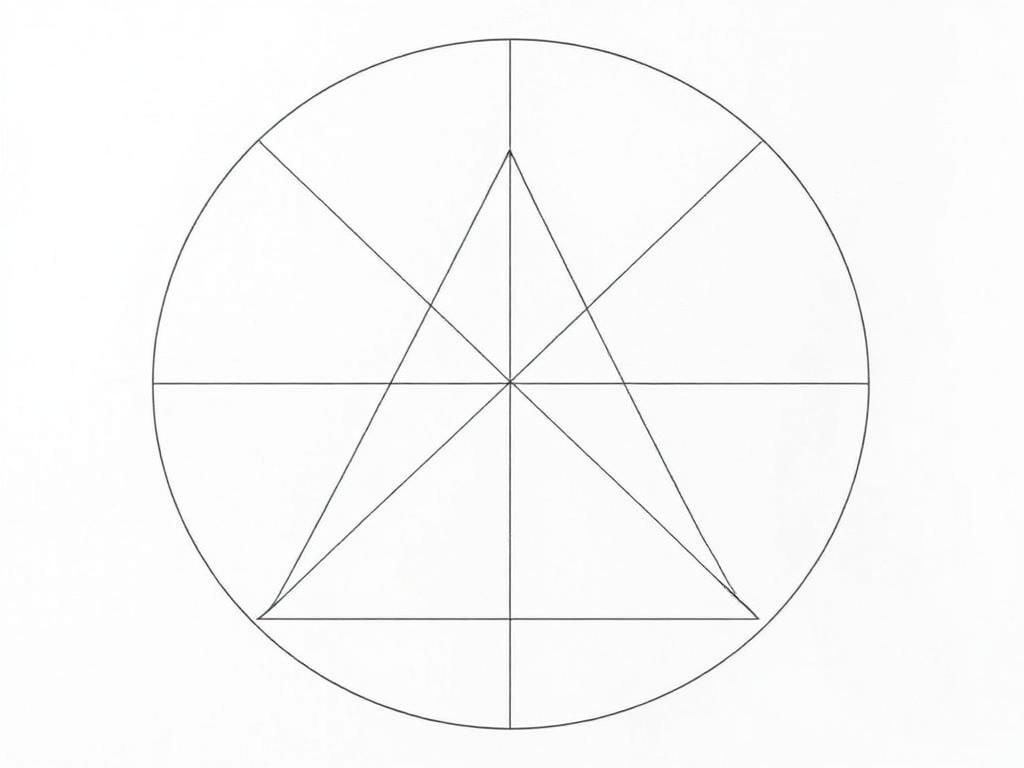
Triangles Inscribed in Circles
When a triangle is inscribed within a circle, it means that all the vertices of the triangle touch the circle. Such triangles possess unique properties worth noting.
– **Definition and Properties**:
An inscribed triangle can be analyzed by its relationship to the circumscribed circle (circumcircle). The center of this circle is known as the circumcenter, which is found at the intersection of the triangles’ perpendicular bisectors.
– **Examples of Inscribed Triangles**:
Consider a right triangle inscribed in a circle. By the Inscribed Angle Theorem, the angle opposite the diameter is a right angle.
Application of the Inscribed Angle Theorem
The Inscribed Angle Theorem states that the angle subtended by an arc at the circumference is half the angle subtended at the center. For example, for a triangle \(ABC\) inscribed in a circle, if \(AB\) subtends arc \(AOB\), then \(∠ACB = 1/2 ∠AOB\).

Circles Inscribed in Triangles
A circle can also be inscribed within a triangle, allowing for another fascinating aspect of the triangle and circle relationship.
– **Definition and Properties**:
The inscribed circle, or incircle, is the largest circle that fits inside the triangle, touching all three sides. The center of this circle is called the incenter, derived from the intersection of the angle bisectors of the triangle.
– **Heron’s Formula for Area**:
To compute the area of a triangle when the lengths of its sides are known, Heron’s formula is used, defined as:
\[
A = \sqrt{s(s-a)(s-b)(s-c)}
\]
where \(s\) is the semi-perimeter \(s = (a+b+c)/2\). The incircle’s radius \(r\) is related to the area \(A\) by \(A = r \times s\).
Geometric Constructions
Constructing a Triangle Given a Circle
Creating a triangle within a circle involves the following steps:
1. Choose the circle’s radius and center: Draw a circle with a chosen radius around a specific center point.
2. Determine triangle vertices using the circle: Select three points on the circumference. Connect these points to form a triangle.
Constructing a Circle Given a Triangle
To circumscribe a circle around a triangle:
1. Find the circumcenter: Construct the perpendicular bisectors of two sides of the triangle until they intersect; this point is the circumcenter.
2. Draw the circumcircle: Use the circumcenter as the circle’s center and the radius equal to the distance from the circumcenter to any triangle vertex.
Practical Applications
Engineering and Architecture
The significance of both the triangle and circle in engineering and architecture cannot be overstated. Triangles provide structural integrity and strength which makes them essential in bridge construction and roofing. Circles, used in domes and arches, offer aesthetic elegance while distributing loads efficiently.
Art and Design
Triangles and circles inspire artistic designs. The harmony created by these shapes is evident in the compositions of artworks and architectural masterpieces. For instance, the pyramids of Egypt exemplify the use of triangular shapes, while domes, like that of St. Peter’s Basilica in Rome, showcase the beauty of circular forms.
Theoretical Concepts
Non-Euclidean Geometry
In non-Euclidean geometry, the behavior of triangles and circles is fascinatingly altered.
– In **spherical geometry**, triangles drawn on a sphere have angles that sum to more than 180 degrees.
– In **hyperbolic geometry**, triangles have angles that sum to less than 180 degrees.
Both types of geometries provide alternate perspectives on the fundamental properties of triangles and circles.
The Golden Ratio
The connection between the triangle and circle extends to the Golden Ratio, a special ratio often found in nature and art. This ratio appears in various forms of triangles and circles, influencing design elements, such as the ratio of the circle’s circumference to its radius, which approximates the Golden Ratio in aesthetics.
Fun Facts and Trivia
– The ancient Greeks revered the properties of triangles and circles, contributing to their understanding of their mathematical nature.
– Did you know? Archimedes, the pioneer mathematician, famously calculated the area of a circle using triangles inscribed within it.
– The relationship between a circle’s circumference and its diameter is a mathematical constant known as π (pi), approximately equal to 3.14.
Conclusion
The triangle and circle not only present intriguing mathematical relationships but also manifest beauty in art and architecture. Their enduring relevance across different disciplines reminds us of the importance of exploring geometric shapes and their properties.
FAQs
1. What are the different types of triangles?
There are three types of triangles: equilateral, isosceles, and scalene, distinguished by their side lengths.
2. What defines a circle?
A circle is defined as the set of all points equidistant from a central point.
3. How do triangles inscribed in circles behave?
Triangles inscribed in circles exhibit properties associated with the arcs and angles they subtend.
4. What is Heron’s formula?
Heron’s formula is used to calculate the area of a triangle when the lengths of its sides are known, expressed as \(A = \sqrt{s(s-a)(s-b)(s-c)}\).
5. How are circles constructed around triangles?
A circle can be constructed around a triangle by finding the circumcenter and then drawing a circle with that center and a radius equal to the distance from the circumcenter to a vertex of the triangle.
6. Why are triangles important in architecture?
Triangles are essential in architecture as they provide structural integrity and stability.
7. What is the significance of the Golden Ratio in circles and triangles?
The Golden Ratio appears in many natural and artistic forms, representing aesthetic beauty often found in the proportions of triangles and circles.
8. How do triangles and circles relate in non-Euclidean geometry?
In non-Euclidean geometry, the properties of triangles and circles differ greatly from Euclidean contexts, altering their fundamental characteristics.
9. Can a triangle have an inscribed circle?
Yes, every triangle can have an inscribed circle, known as the incircle, which touches all three sides.
10. What interesting facts exist about triangles and circles in history?
Ancient civilizations across cultures recognized the mathematical significance of triangles and circles, leading to concepts that laid the groundwork for modern geometry.
| Concept | Description | Example |
|---|---|---|
| Triangle Types | Equilateral, Isosceles, Scalene | Equilateral: ABC with sides AB = AC = BC |
| Circle Properties | Key terms: Radius, Diameter, Circumference, Area | Radius = 5, Diameter = 10, C = 31.4, A = 78.5 |
| Inscribed Triangle | Triangle inside a circle | Right triangle ABC inscribed in a circle |
| Circumscribed Circle | Circle around a triangle | Circumcircle around triangle DEF |
